Fibonacci Series in Constant Time Complexity O(1) [4]

The Fibonacci sequence is a well-known mathematical series where each number is the sum of the two preceding ones, starting from 0 and 1.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, .....

So the simple method to find the nth fibonacci number will be:

F(n) = F(n-1) + F(n-2)

where

• F() is the Fibonacci function
• n is the number of the sequence to find

Now if someone asks to write the code to find the nth fibonacci number what will you do?

Well the most common approach is to use recursion or iteration to find the nth fibonacci number. But these approaches are not efficient for large values of n. There are also some other approaches like matrix exponentiation which are efficient but they are not constant time complexity. For constant time complexity, we can use a mathematical formula to find the nth fibonacci number.

1. Using Recursive Approach

The recursive method is the most intuitive approach to compute Fibonacci numbers. It works by breaking down the problem into smaller sub-problems, with the base cases being F(0) = 0 and F(1) = 1.

1. Code Implementation:

cpp
1.
#include <iostream>
2.
using namespace std;
3.

4.
long long fibonacciRecursive(int n) {
5.
    if (n <= 1)
6.
        return n; // Base case
7.
    return fibonacciRecursive(n - 1) + fibonacciRecursive(n - 2);
8.
}
9.

10.
int main() {
11.
    int n = 10; // Example input
12.
    cout << "Fibonacci(" << n << ") using recursion: " << fibonacciRecursive(n) << endl;
13.
    return 0;
14.
}

2. How It Works:

• Each function call calculates F(n - 1) and F(n - 2) until it reaches the base cases.
• For n = 10, the function calls follow a tree-like structure, with overlapping sub-problems.

3. Complexity:

• Time Complexity: O(2^n), because each call generates two additional recursive calls.
• Space Complexity: O(n), due to the stack space used in recursive calls.

4. Limitations:

• Exponential time complexity makes it impractical for large n.
• Redundant calculations lead to inefficiency.

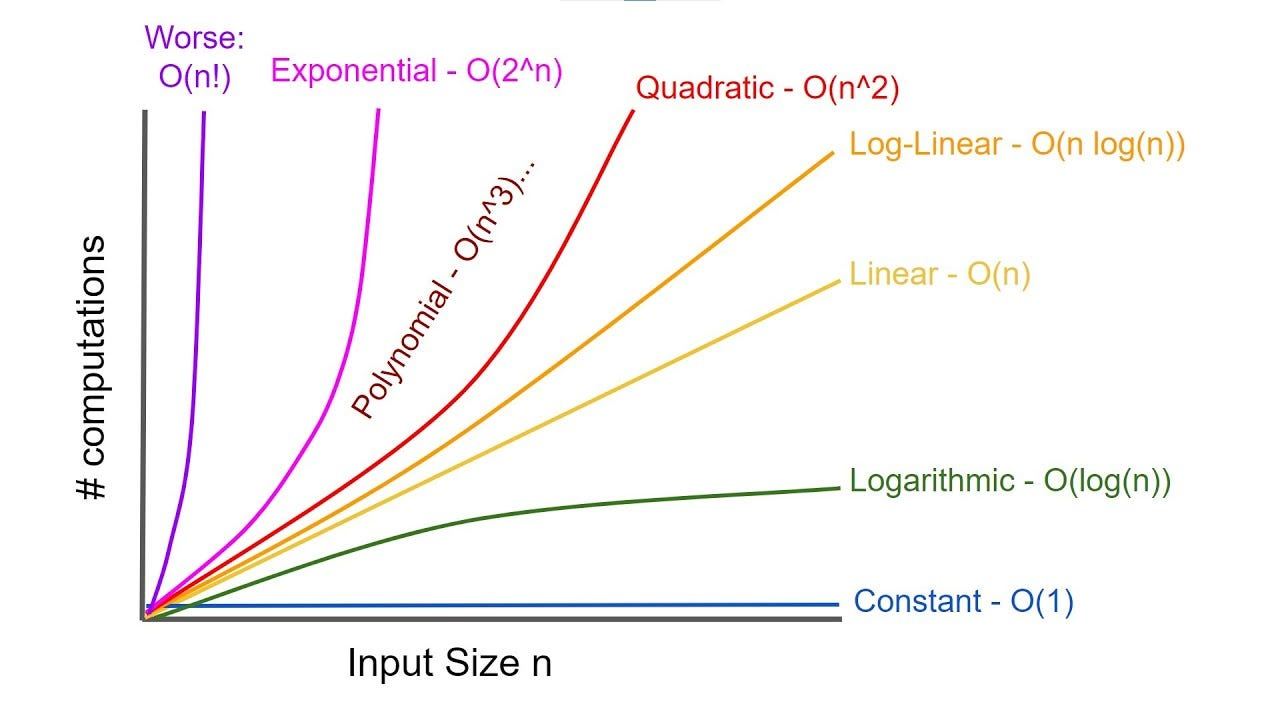
In the graph above, the recursive method's time complexity grows exponentially with n, making it unsuitable for large values. Let's explore more efficient methods to compute Fibonacci numbers.

2. Iterative Method (Using a Loop)

To overcome the inefficiency of recursion, an iterative method can be used. This approach calculates Fibonacci numbers in a linear manner, storing only the previous two values at each step.

1. Code Implementation:

cpp
1.
#include <iostream>
2.
using namespace std;
3.

4.
long long fibonacciIterative(int n) {
5.
    if (n <= 1)
6.
        return n; // Base case
7.

8.
    long long a = 0, b = 1, c;
9.
    for (int i = 2; i <= n; i++) {
10.
        c = a + b; // Calculate the next Fibonacci number
11.
        a = b;     // Update previous numbers
12.
        b = c;
13.
    }
14.
    return b;
15.
}
16.

17.
int main() {
18.
    int n = 10; // Example input
19.
    cout << "Fibonacci(" << n << ") using iteration: " << fibonacciIterative(n) << endl;
20.
    return 0;
21.
}

2. How It Works:

• Start with F(0) = 0 and F(1) = 1.
• Use a loop to calculate F(2) through F(n), updating the previous values at each step.

3. Complexity:

• Time Complexity: O(n), as it computes each Fibonacci number up to n.
• Space Complexity: O(1), as only a constant amount of memory is used.

4. Advantages:

• Efficient for moderate values of n.
• Avoids the overhead of recursive calls.

Since, the iterative method has a linear time complexity, it is more efficient than the recursive method for large values of n. However, for very large values of n, the iterative method may still be slow as given in above graph.

3. Mathematical Formula (Constant Time O(1))

The most efficient way to compute Fibonacci numbers is by using Binet's Formula, which leverages the golden ratio Φ. This method allows direct calculation without iteration or recursion.

1. Binet's Formula:

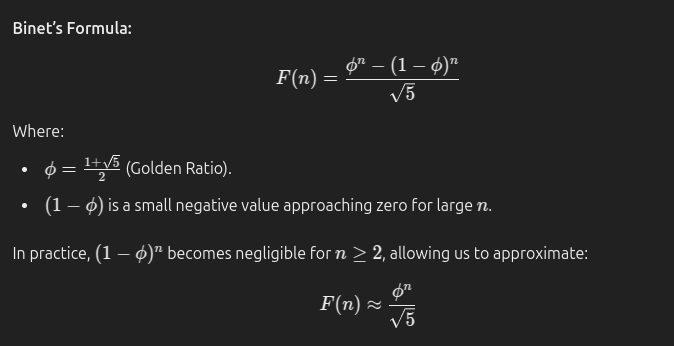
2. Code Implementation:

cpp
1.
#include <iostream>
2.
#include <cmath>
3.
using namespace std;
4.

5.
unsigned long long fibonacciFormula(int n)
6.
{
7.
  double phi = (1 + sqrt(5)) / 2;      // Golden ratio
8.
  return round(pow(phi, n) / sqrt(5)); // Use rounding to handle precision
9.
}
10.

11.
int main()
12.
{
13.
  int n = 80; // Example input
14.
  cout << "Fibonacci(" << n << ") using formula: " << fibonacciFormula(n) << endl;
15.
  return 0;
16.
}

3. How It Works:

• The formula directly calculates the n-th Fibonacci number using powers of the golden ratio.
• The round() function is used to handle precision errors due to floating-point arithmetic.

4. Complexity:

• Time Complexity: O(1), as it involves a fixed number of mathematical operations regardless of n.
• Space Complexity: O(1), requiring only a constant amount of memory.

5. Advantages:

• The fastest method for computing Fibonacci numbers.
• Ideal for applications where speed is critical, such as competitive programming.

6. Limitations:

• May lose precision for very large n due to floating-point calculations.
• Suitable for n within the range of standard data types.

7. Comparison of Methods

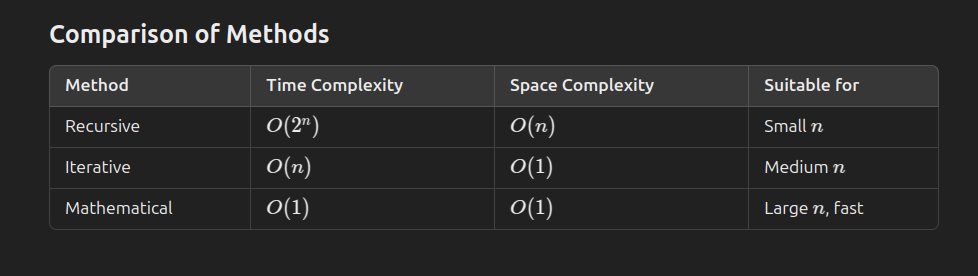
8. Conclusion

• Recursive Approach: Simple but inefficient due to redundant calculations.
• Iterative Approach: More efficient, with linear complexity, but still limited for very large n.
• Mathematical Formula: The ultimate solution for constant time complexity, best for large n where speed is critical.

When calculating Fibonacci numbers for very large n, be cautious of integer overflow in C++. Standard data types like int and long may overflow for large Fibonacci values. Even long long has limitations. To handle large numbers, you can use types like unsigned long long or libraries like GMP for arbitrary precision arithmetic. Additionally, when using Binet's formula, floating-point precision may lead to rounding errors for very large n. Always choose appropriate data types or libraries to avoid overflow and ensure accuracy.

For small to medium n, iteration is often sufficient. For large n, the mathematical formula is the go-to solution.

Happy coding! 🚀