Asymptotic Notation - Big O, Big Theta (Θ), and Big Omega (Ω) [03]

1. Introduction

Asymptotic notation is a mathematical tool used to describe the behavior of algorithms as their input size grows. These notations help us understand and compare algorithm efficiency without getting bogged down by hardware-specific details or smaller implementation variations.

2. Big O Notation (O)

1. Definition

Big O notation represents the upper bound or worst-case scenario of an algorithm's growth rate. It describes the maximum amount of time or space an algorithm might need.

2. Key Characteristics

• Represents the upper limit of growth
• Provides a "less than or equal to" relationship
• Most commonly used in practice due to its focus on worst-case scenarios
• Written as O(f(n)) where f(n) is the growth function

3. Practical Meaning

If an algorithm is O(f(n)), its resource usage will never grow faster than f(n), though it might grow more slowly. Think of it as a ceiling or maximum limit on growth.

4. Example Scenarios

• When describing the worst possible runtime
• When analyzing algorithms that have varying performance based on input
• When you need to guarantee that an algorithm won't exceed certain resource bounds

3. Big Omega Notation (Ω)

1. Definition

Big Omega represents the lower bound or best-case scenario of an algorithm's growth rate. It describes the minimum amount of time or space an algorithm will need.

2. Key Characteristics

• Represents the lower limit of growth
• Provides a "greater than or equal to" relationship
• Less commonly used in practice but important for theoretical analysis
• Written as Ω(f(n)) where f(n) is the growth function

3. Practical Meaning

If an algorithm is Ω(f(n)), its resource usage will never grow slower than f(n), though it might grow more quickly. Think of it as a floor or minimum limit on growth.

4. Example Scenarios

• When describing the best possible runtime
• When proving lower bounds for problems
• When analyzing algorithms that have a minimum resource requirement

4. Big Theta Notation (Θ)

1. Definition

Big Theta represents both the upper and lower bounds of an algorithm's growth rate. It describes the exact growth rate when the upper and lower bounds match.

2. Key Characteristics

• Represents both upper and lower limits simultaneously
• Provides an "equal to" relationship
• Most precise of the three notations
• Written as Θ(f(n)) where f(n) is the growth function
• Only exists when Big O and Big Omega match

3. Practical Meaning

If an algorithm is Θ(f(n)), its resource usage will grow exactly at the rate of f(n), within constant factors. Think of it as a tight bound or exact growth rate.

4. Example Scenarios

• When describing algorithms with consistent performance
• When the best and worst cases are the same
• When analyzing fundamental operations that always take the same amount of time

5. Relationships Between Notations

1. If an algorithm is Θ(f(n)), it is also both O(f(n)) and Ω(f(n))
2. O(f(n)) only provides an upper bound and could be a loose estimate
3. Ω(f(n)) only provides a lower bound and could be a loose estimate
4. Θ(f(n)) is the most precise as it provides both bounds

6. Common Growth Rates (From Fastest to Slowest)

1. Constant Growth: O(1)
2. Logarithmic Growth: O(log n)
3. Linear Growth: O(n)
4. Linearithmic Growth: O(n log n)
5. Quadratic Growth: O(n²)
6. Cubic Growth: O(n³)
7. Exponential Growth: O(2ⁿ)
8. Factorial Growth: O(n!)

7. Practical Implications

1. When to Use Each Notation

• Use Big O (O) when:
  • Analyzing worst-case scenarios
  • Providing performance guarantees
  • Comparing algorithms' efficiency
• Use Big Omega (Ω) when:
  • Analyzing best-case scenarios
  • Proving lower bounds
  • Demonstrating minimum resource requirements
• Use Big Theta (Θ) when:
  • The algorithm's performance is consistent
  • You can prove matching upper and lower bounds
  • You need to describe exact growth behavior

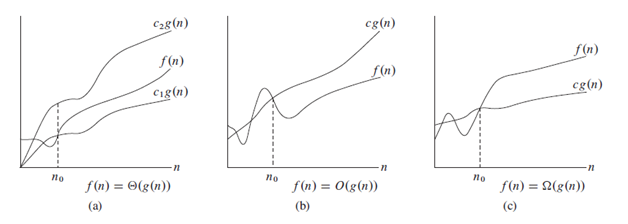
8. Conclusion

Understanding these three notations is crucial for algorithm analysis:

• Big O gives us the upper bound (worst case)
• Big Omega gives us the lower bound (best case)
• Big Theta gives us exact bounds (when they match)

Together, they provide a complete framework for describing and analyzing algorithm efficiency, helping us make informed decisions about algorithm selection and optimization.