Time Complexity and Big O Notation [02]

Understanding time complexity and Big O notation is crucial for writing efficient code and becoming a better programmer. In this blog post, we'll dive deep into these concepts, learn how to analyze algorithms, and see practical examples using C++.

2. What is Time Complexity?

Time complexity is a way to measure how an algorithm's runtime grows as the input size increases. Or simply, Time complexity is the study of efficiency of algorithm. Rather than measuring actual time in seconds (which varies based on hardware), we count the number of elementary operations performed by the algorithm.

Consider these two C++ functions that find the sum of numbers from 1 to n:

cpp
1.// Method 1: Using a loop
2.int sumUsingLoop(int n) {
3.    int sum = 0;
4.    for (int i = 1; i <= n; i++) {
5.        sum += i;
6.    }
7.    return sum;
8.}
9.
10.// Method 2: Using mathematical formula
11.int sumUsingFormula(int n) {
12.    return (n * (n + 1)) / 2;
13.}

While both functions give the same result, they have very different time complexities. The first function runs n times, while the second performs just three operations regardless of n.

3. Understanding Big O Notation

Big O notation describes the upper bound of the growth rate of an algorithm. It's written as O(f(n)), where f(n) represents the growth rate function.

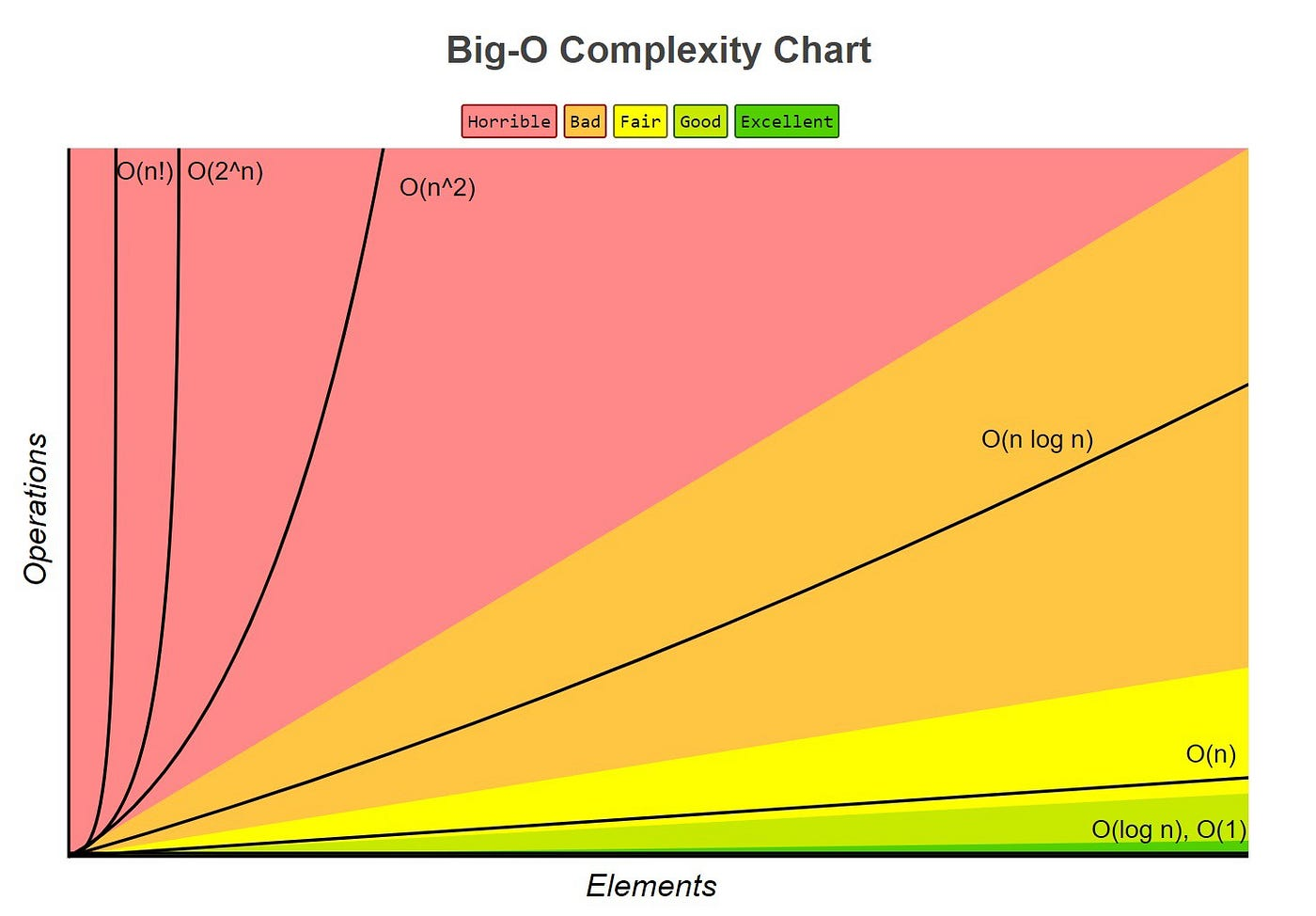
Common Big O complexities (from fastest to slowest):

O(1) - Constant time
O(log n) - Logarithmic time
O(n) - Linear time
O(n log n) - Linearithmic time
O(n²) - Quadratic time
O(2ⁿ) - Exponential time

1. O(1) - Constant Time

Operations that don't depend on input size:

cpp
1.int getFirstElement(vector<int>& arr) {
2.    if (arr.empty()) return -1;
3.    return arr[0];
4.}

2. O(n) - Linear Time

Operations that scale linearly with input:

cpp
1.bool linearSearch(vector<int>& arr, int target) {
2.    for (int num : arr) {
3.        if (num == target) return true;
4.    }
5.    return false;
6.}

3. O(log n) - Logarithmic Time

Operations that reduce the problem size by half each time:

cpp
1.int binarySearch(vector<int>& arr, int target) {
2.    int left = 0;
3.    int right = arr.size() - 1;
4.    
5.    while (left <= right) {
6.        int mid = left + (right - left) / 2;
7.        if (arr[mid] == target) return mid;
8.        if (arr[mid] < target) left = mid + 1;
9.        else right = mid - 1;
10.    }
11.    return -1;
12.}

4. O(n²) - Quadratic Time

Nested iterations over the input:

cpp
1.void bubbleSort(vector<int>& arr) {
2.    int n = arr.size();
3.    for (int i = 0; i < n - 1; i++) {
4.        for (int j = 0; j < n - i - 1; j++) {
5.            if (arr[j] > arr[j + 1]) {
6.                swap(arr[j], arr[j + 1]);
7.            }
8.        }
9.    }
10.}

Complexity Chart

4. How to Calculate Time Complexity

Follow these steps to analyze an algorithm:

Count the operations in the innermost part of your code
Multiply by the number of times each loop runs
Keep only the highest-order term
Drop constants and coefficients

1. Example Analysis

Let's analyze this function:

cpp
1.void findPairs(vector<int>& arr) {
2.    int n = arr.size();
3.    
4.    // Print all pairs
5.    for (int i = 0; i < n; i++) {           // Runs n times
6.        for (int j = i + 1; j < n; j++) {   // Runs (n-i) times
7.            cout << arr[i] << "," << arr[j] << endl;
8.        }
9.    }
10.}

Analysis:

Inner loop runs (n-i) times for each i
Total operations: Σ(n-i) from i=0 to n-1
This sum equals n(n-1)/2
Simplifying and keeping highest order: O(n²)

5. Common Pitfalls

1. Adding vs. Multiplying Complexities

cpp
1.// O(n + m) - Two separate loops
2.void process(vector<int>& arr1, vector<int>& arr2) {
3.    for (int num : arr1) { /* O(n) */ }
4.    for (int num : arr2) { /* O(m) */ }
5.}
6.
7.// O(n * m) - Nested loops
8.void process2(vector<int>& arr1, vector<int>& arr2) {
9.    for (int num1 : arr1) {      // O(n)
10.        for (int num2 : arr2) {  // O(m)
11.            // Process pair
12.        }
13.    }
14.}

2. Hidden Loops

Remember that some C++ operations have their own complexities:

vector.push_back() - Usually O(1), but can be O(n) when resizing
unordered_map.find() - O(1) average, O(n) worst case
sort() - O(n log n)

6. Best Practices for Writing Efficient Code

Choose appropriate data structures
- Use unordered_map instead of map when order doesn't matter
- Use vector instead of list for sequential access
Avoid unnecessary nested loops
- Use hash tables for lookup operations
- Consider preprocessing data when possible
Look for mathematical solutions
- Like our initial sum example, mathematical formulas often provide O(1) solutions

7. Conclusion

Understanding time complexity and Big O notation is essential for writing efficient code. When designing algorithms, always consider:

The size of your input
The worst-case scenario
The trade-off between time and space complexity
Whether a more efficient solution exists

Remember that the fastest algorithm isn't always the best choice - consider factors like code readability, maintenance, and the actual size of your input data.

8. Practice Problems

To solidify your understanding, try analyzing the time complexity of these functions:

cpp
1.// Problem 1
2.int mystery1(int n) {
3.    int result = 0;
4.    for (int i = 1; i <= n; i *= 2) {
5.        result += i;
6.    }
7.    return result;
8.}
9.
10.// Problem 2
11.void mystery2(vector<int>& arr) {
12.    int n = arr.size();
13.    for (int i = 0; i < n; i++) {
14.        for (int j = i; j < n; j++) {
15.            for (int k = i; k <= j; k++) {
16.                cout << arr[k] << " ";
17.            }
18.            cout << endl;
19.        }
20.    }
21.}

(Solutions: mystery1 is O(log n), mystery2 is O(n³))

Remember: The best way to understand time complexity is through practice. Try analyzing different algorithms and writing your own solutions with efficiency in mind.